The Monty Hall Problem and The Destiny of Humankind

Or, How I Learned to Stop Worrying and Love That I Was Stupid

Do you know the Monty Hall problem? It’s a math problem loosely based on the popular 1970s game show Let’s Make a Deal, hosted by Monty Hall.

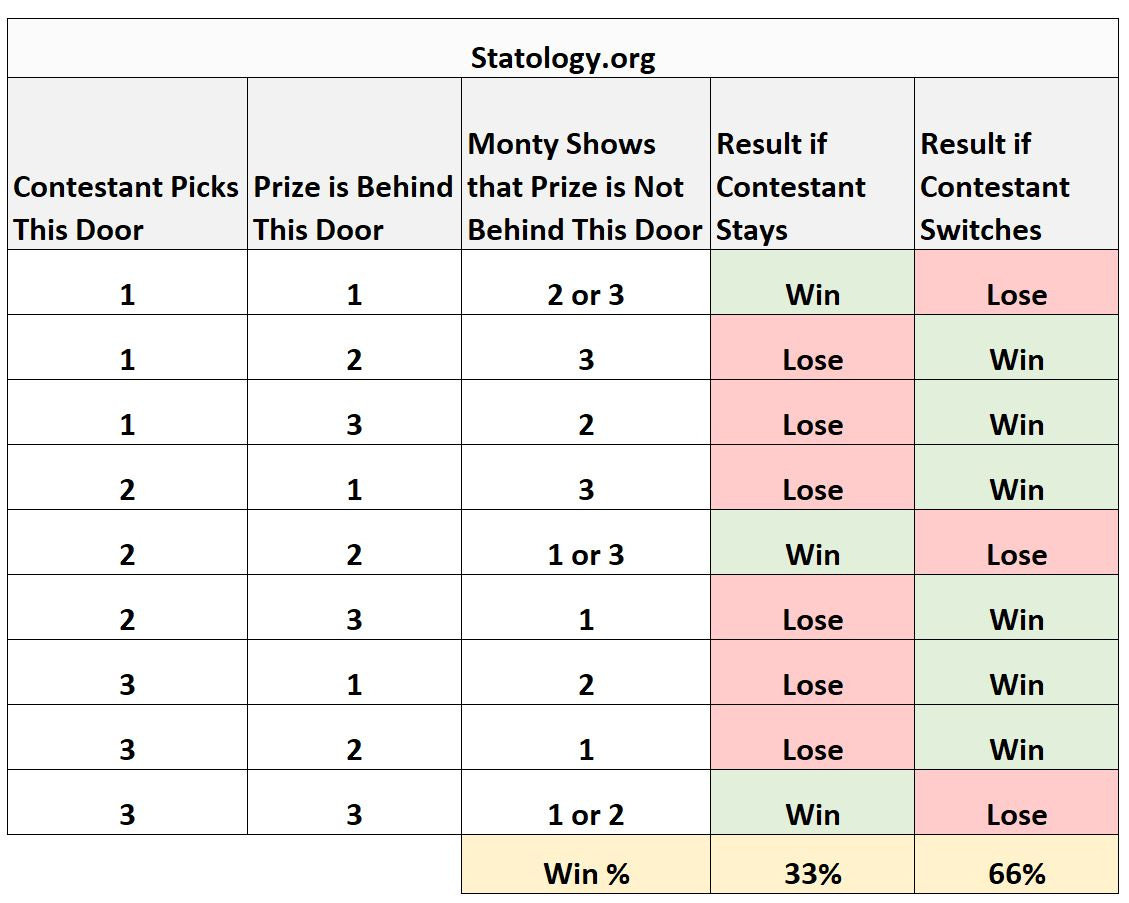
Here’s how it goes. There are three doors, labeled A, B, and C. Behind one of the doors is a car; behind the other two doors are goats. Monty knows where the car is. As a contestant, Monty asks you to pick a door, and if you pick the right door, you win the car.

Let’s say you pick A. Before Monty reveals what’s behind Door A, he’s going to reveal one of the incorrect doors — let’s say it’s Door B. He opens the door, and sure enough, there’s a goat. Now Monty gives you a choice: you can stick with your original choice, or you can switch to Door C. Which do you choose?

The answer is that you should switch.

But wait. That doesn’t seem right. Once Monty takes away one door, don’t you have a fifty-fifty shot of winning the car? Why switch your pick? How does it matter?

Here’s how Jim Holt puts it in his essay collection, When Einstein Walked With Gödel:

When you initially chose Door A, there was a 1/3 chance that you would win the car. Monty’s crafty revelation that there’s a goat behind Door B furnishes no new information about what’s behind the door you already chose — you already know one of the other two doors has to conceal a goat — so the likelihood that the car is behind Door A remains one-third. Which means that with Door B eliminated, there is a two-thirds chance the car is behind Door C.

Maybe all this makes immediate sense to you. It didn’t make any sense to me. I read Holt’s breakdown a few times, watched a YouTube explainer, and still didn’t really get it. I’m well aware how bad I am at math, but this problem seemed like the starkest, harshest indictment of my numerical illiteracy to date. I’d harbored suspicions before, but now I had to consider the serious possibility that I’d never grasped some fundamental fourth grade math lesson — the equivalent to never having learned how to tie my shoes properly or wear pants in the forward-facing position. Just how stupid was I — am I?

As it turns out, most people get the Monty Hall problem wrong. Though earlier variations exist, including the Three Prisoners problem, it was Marilyn vos Savant who made it famous in a 1990 Parade column.¹ After vos Savant claimed that participants should always switch doors, she received around 10,000 letters, most in protest, including thousands signed by academics and professors. Holt singles out Paul Erdős, “one of the supreme mathematicians of the last century,” who insisted vos Savant’s answer was wrong. It took a friend running a computer simulation to convince him otherwise.

So again, how does this uniquely counterintuitive puzzle work? Here’s Marilyn’s reasoning:

Suppose there are a million doors, and you pick door No. 1. Then the host, who knows what’s behind the doors, and will always avoid the one with the prize, opens them all except door #777,777. You’d switch to that door pretty fast, wouldn’t you?

The most important fact is that the host knows where the car is. If the host, or Monty, didn’t know the location of the car then opened up a goat door, your chances would indeed be fifty-fifty. But because Monty does know the location of the car and will never reveal it until the game is over, he is doing you a small favor. He is telling you something about the other doors. You won’t learn anything about your door until the game is over. But you will always learn about the other doors: learning about the other doors, in effect, is the game.

If I’m not making sense, and I’m probably not, Marilyn’s scaled-up scenario is especially helpful. By expanding the game to a million doors, she reveals the logic at play. Monty is going to open 999,998 doors knowing perfectly well that a goat is behind every single one. But there is one door other than yours that he has chosen not to open, and you can be 99.9% sure there’s a car behind it. As Marilyn says, “You’d switch…wouldn’t you?”

A year after the original Parade article, Monty Hall ran an experiment at his Beverly Hills home that proved vos Savant’s answer correct and made the front page of the New York Times. All the news that’s fit to print!

Well, would you? The game hinges on that delectable psychological tease, which the host of Let’s Make a Deal knew better than anyone. “By opening that door we were applying pressure,” Hall told the New York Times in 1991. “We called it the Henry James treatment. It was The Turn of the Screw.”² As a participant, once the game is down to two doors, you’re going to get excited, maybe a little overeager. You’re almost there! Maybe you actually picked the right door! Don’t waver now! Have a little faith in yourself!

But the appearance of “almost there” is an illusion. Your odds remain one in three, and you still probably didn’t pick the right door. That’s when I finally understood what was going on: when I recognized that my first choice is always probably, mathematically, wrong — and nothing in the game will ever change that fact. Even when only two doors are left, my door is still in all likelihood wrong. Contrary to what the game may fool me into believing, I have not overcome human nature; human nature remains the same. It’s the game that has changed, and if I don’t recognize that change, the game will work against me.³

So, yes, I am stupid, but so are most people. What’s more, having a greater appreciation of one’s stupidity is at least one way to unlock the puzzle. Returning to Holt’s essay, he connects the problem to overconfidence. While everyone exhibits overconfidence to some degree, a study in the Journal of Personality and Social Psychology demonstrates that the incompetent have it in spades: “Not only do they reach erroneous conclusions and make unfortunate choices, but their incompetence robs them of the ability to realize it” (a truth as responsible for King Lear as much as that other famous Monty, Python). At the same time, the competent aren’t off the hook: “the more specialized information you have about something, the more likely you are to be overconfident in your judgment about it.” Hence why, in addition to run-of-the-mill sexism, thousands of academics not only disagreed with vos Savant but also felt compelled to mail letters explaining why she was wrong (never mind that, in keeping with her name, vos Savant held the highest IQ recorded in the Guinness Book of Records).⁴

All of this makes me wonder whether the Monty Hall problem is even more profound than we suspect. What other fundamental truths does it reveal? It’s risky, and probably a little too cute, to draw existential claims from math equations, but let’s try it out as a thought experiment.

Does the Monty Hall problem describe an ethic? Does it describe a principle? I would argue that it does describe what Holt calls in another essay the Copernican principle — essentially, “you’re not special.”

But let’s go further. Does the problem describe a dharma? A Dao? A theology? I’ll restate the issue, this time in a slightly different way.

With limited information, we are forced to make a choice. Fine; we can live with our decision for now. We are only midway through the game. But then we are given a little more information, and a second chance — a last chance. What do we do? We know more than we did before, but we’re being pulled in opposite directions: the old way, our original way, which is the more comfortable one; or the new way, not our first choice, and so more uncomfortable. In either case there are no guarantees: a guarantee would render the whole situation pointless. It’s evidently not pointless, but we can’t be certain of our decision. Still, if we can’t be certain of our decision, does that mean our decision is arbitrary? Just a random shot in the dark? Oddly enough, no, because we know more than we knew before, and the knowledge we’ve been given isn’t arbitrary. In fact, it’s the opposite: the knowledge we’ve been given, the screw we’ve seen turned, has transformed the entire situation. It’s decisive. Or should be.

Unfortunately, we’re bad at making decisions. We have a prejudice for being wrong. Even when we’re offered help and even if the decision is — rationally speaking — obvious, we seem determined to miss the mark. In other words we are, to varying degrees, stupid, and the result is often, to varying degrees, tragic. But not exclusively tragic. Because there is always a chance for comedy.

For example, let’s say we stick with our original choice, as most people tend to do. If it turns out to be wrong, the verdict is pretty cut and dry. We made the wrong choice. But if we stick with our original choice and our original choice turns out to be right, we’ve actually still made the wrong decision within the logic of the game. There’s no reason we should have stayed. Our reward is only the result of dumb luck (if that’s the right phrase). We’ve won, but we didn’t deserve it.

In which case, with a few adjustments and clarifications, we could call this universal and intractable phenomenon the Monty Hall Problem of Sin and Grace.

1. Here’s where it’s important to note that the Monty Hall problem is hypothetical: the game wasn’t actually played this way, presumably because it would’ve cost the show too many cars.

2. A sharp insight from Mr. Hall, and a serendipitous opportunity to remind you that the other Mr. Hall — that is, yours truly — will be blogging through The Turn of the Screw in October. Act now to purchase your copy and read along!

3. To crib from The Wire.

4. What remains a mystery is why so many PhDs in the ’90s were reading Parade.